HOMBRE DE VITRUVIO
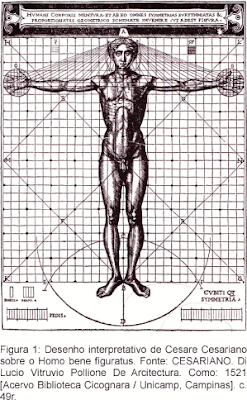
El Hombre de Vitruvio es el dibujo realizado por Leonardo da Vinci alrededor del año 1492 en uno de sus diarios y que se acompaña de notas anatómicas. El dibujo está realizado en lápiz y tinta y mide 34,2 x 24,5 cm. En la actualidad forma parte de la colección de la Galería de la Academia de Venecia.
Se trata de un estudio de las proporciones del cuerpo humano, realizado a partir de los textos del arquitecto romano Vitruvio titulados -Vitruvii De Architectura-, y del que el dibujo toma su nombre.
Las notas de Leonardo da Vinci que acompañan el dibujo determinan las proporciones del cuerpo humano de acuerdo con el texto antiguo de Vitruvio:
-Una palma es la anchura de cuatro dedos.
-Un pie es la anchura de cuatro palmas.
-Un antebrazo es la anchura de seis palmas.
-La altura de un hombre son cuatro antebrazos (24 palmas).
-Un paso es igual a cuatro antebrazos.
-La longitud de los brazos extendidos de un hombre es igual a su altura.
-La distancia entre el nacimiento del pelo y la barbilla es un décimo de la altura de un hombre.
-La altura de la cabeza hasta la barbilla es un octavo de la altura de un hombre.
-La distancia entre el nacimiento del pelo a la parte superior del pecho es un séptimo de la altura de un hombre.
-La altura de la cabeza hasta el final de las costillas es un cuarto de la altura de un hombre.
-La anchura máxima de los hombros es un cuarto de la altura de un hombre.
-La distancia del codo al extremo de la mano es un quinto de la altura de un hombre.
-La distancia del codo a la axila es un octavo de la altura de un hombre.
-La longitud de la mano es un décimo de la altura de un hombre.
-La distancia de la barbilla a la nariz es un tercio de la longitud de la cara. -La distancia entre el nacimiento del pelo y las cejas es un tercio de la longitud de la cara.
-La altura de la oreja es un tercio de la longitud de la cara.
Leonardo tuvo acceso a escritos que guardaban secretos y conocimientos de la antigüedad y conocía el peligro que tenía revelar alguno de los secretos a los que él tuvo acceso, por ello muchas de sus anotaciones particulares, y algunas de sus obras públicas, están realizadas en una clave secreta que permite ocultar a la vista general la información que el artista plasma para un futuro lector, y que con la clave indicada, podrá descifrar en su momento.
Leonardo muestra a través de sus dibujos su maestría en la composición, claridad de expresión y fundamentalmente, un profundo conocimiento de la antigüedad romana, sus investigaciones sobre los textos de Vitruvio y la geometría permite asegurar que tenía un intenso conocimiento sobre la ciencia antigua y sus enseñanzas.
Y es en la ciencia de la arquitectura donde se guarda el saber de la antigüedad. Desglosar el saber y conocimiento que Leonardo atesoraba a través de los textos de Vitruvio no tiene porque parecer forzado, muy al contrario, Leonardo se identifica de manera completa con el arquitecto romano, y con toda seguridad fue entendedor de todas las enseñanzas de su lejano maestro en el tiempo.
El texto original de Vitruvio y que inspiró a Leonardo el dibujo donde se representa a sí mismo dentro de un círculo y un cuadrado nos remite directamente a que él creía haber alcanzado el secreto de la "cuadratura del círculo".
Dice Vitruvio en su libro tercero cuando trata del origen de las medidas de los templos:
Es imposible que un templo posea una correcta disposición si carece de simetría y de proporción, como sucede con los miembros o partes del cuerpo de un hombre bien formado.
El cuerpo humano lo formo la naturaleza de tal manera que el rostro, desde la barbilla hasta la parte mas alta de la frente, donde están las raíces del pelo, mida una décima parte de su altura total. La palma de la mano, desde la muñeca hasta el extremo del dedo medio, mide exactamente lo mismo; la cabeza, desde la barbilla hasta su coronilla, mide una octava parte de todo el cuerpo; una sexta parte mide desde el esternón hasta las raíces del pelo y desde la parte media del pecho hasta la coronilla, una cuarta parte.
Desde el mentón hasta la base de la nariz, mide una tercera parte y desde las cejas hasta las raíces del pelo, la frente mide igualmente otra tercera parte. Si nos referios al pie, equivale a una sexta parte de la altura del cuerpo; el codo, una cuarta parte, y el pecho equivale igualmente a una cuarta parte.
Los restantes miembros guardan también una proporción de simetría, de la que se sirvieron los antiguos pintores y escultores famosos, alcanzando una extraordinaria consideración y fama. Exactamente de igual manera, las partes de los templos deben guardar una proporción de simetría perfectamente apropiada de cada una de ellas respecto al conjunto total en su completa dimensión.
El ombligo es el punto central natural del cuerpo humano. En efecto, si se coloca un hombre boca arriba, con sus manos y sus pies estirados, situando el centro del compás en su ombligo y trazando una circunferencia, esta tocaría la punta de ambas manos y los dedos de los pies.
La figura circular trazada sobre el cuerpo humano nos posibilita el lograr también un cuadrado: si se mide desde la planta de los pies hasta la coronilla, la medida resultante será la misma que se da entre las puntas de los dedos con los brazos extendidos; exactamente su anchura mide lo mismo que su altura, como los cuadrados que trazamos con la escuadra.
Por tanto, si la naturaleza ha formado el cuerpo humano de modo que sus miembros guardan una exacta proporción respecto a todo el cuerpo, los antiguos fijaron también esta relación en la realización completa de sus obras, donde cada una de sus partes guarda una exacta y puntual proporción respecto a la forma total de su obra.
Dejaron constancia de la proporción de las medidas en todas sus obras, pero sobre todo las tuvieron en cuenta en la construcción de los templos de los dioses, que son un claro reflejo para la posteridad de sus aciertos y logros, como también de sus descuidos y negligencias.
-Vitruvii De Architectura, Libro Tercero-Capítulo I-
Tales/Escalas
Traza con la herramienta "Lápiz" en la Playa de Famara un 
Podemos coger un segmento, por ejemplo 13,6, y multiplicarlo por 1,618, de esta forma tenemos el segmento menor y el segmento medio. A continuación podemos por el teorema de Thales transformarlos de manera que la suma de ambos se transformen en el segmento medio y el segmento medio se transforme en el menor.
profesor del IES Campo Charro-Salamanca
Hay cursos gratuitos (3D BLENDER)